Wer war nicht schon mal auf einer Geburtstagsparty mit 23 Gästen eingeladen und hat sich darüber ereifert, dass dort in mehr als 50% der Fälle zwei Gäste mit dem gleichen Geburtstag weilen? Obwohl sich diese Behauptung für Mathe-Laien abenteuerlich anhört, ist sie mit statistischen Bordmitteln relativ einfach zu beweisen. Dabei kommt es auf die genaue Formulierung des Problems an, niemand kann behaupten, auf eine Party mit 23 Leuten zu gehen und dort mit 50 Prozent Wahrscheinlichkeit jemanden mit seinem Geburtstag zu treffen. Das unerwartete Ergebnis kommt dadurch zustande, dass sich N Gäste untereinander, also jeder mit jeweils N-1 anderen Gästen vergleichen, und dass so ein Paar zustande kommt, das im gleichen Monat und am gleichen Tag (der Jahrgang bleibt unberücksichtigt) Geburtstag hat, ist viel wahrscheinlicher als wenn man nur seinen eigenen Geburtstag mit dem von N-1 Gästen vergleicht.
Wie hoch ist die Wahrscheinlichkeit, dass auf einer Party mit nur zwei Gästen beide am gleichen Tag Geburtstag feiern? Mit einem zur Vereinfachung als 365 Tage lang angenommenen Jahr, ohne Berücksichtigung von saisonalen Geburtsschwankungen oder Spezialfällen wie Zwillingsparties, tritt dies in einem von 365 Fällen auf. Umgekehrt beträgt die Wahrscheinlichkeit, dass beide Gäste an unterschiedlichen Tagen Geburtstag haben, 364/365. Gesellt sich nun zu dem Pärchen ein weiterer Gast hinzu, setzt sich die Wahrscheinlichkeit, dass niemand im Raum am gleichen Tag Geburtstag feiert, aus dem Zusammentreffen zweier voneinander unabhängiger Ereignisse zusammen: Aus dem ersten Ereignis der vorhergehenden Runde mit der Wahrscheinlichkeit 364/365 und einem zweiten, nämlich dass die hinzugekommene Person weder mit der ersten noch der zweiten Person Geburtstag hat, also nur an 363 von 365 Tagen Geburtstag feiern kann. Die Gesamtwahrscheinlichkeit verschiedener Geburtstage von drei Personen ermittelt der Statistiker durch Multiplikation der Wahrscheinlichkeiten der voneinander unabhängigen Einzelereignisse, also 364/365 * 363/365, oder etwa 0,991795. Das umgekehrte Ereignis, also der Fall, dass zwei oder mehr Personen am gleichen Tag Geburtstag feiern, ergibt sich mit einer Wahrscheinlichkeit von 1 - 0,991795, also 0,008205.
| |
| Abbildung 1: Auf einer Party mit 23 Leuten besteht eine Wahrscheinlichkeit von über 50%, dass zwei Gäste den gleichen Geburtstag haben. Bild: Wikipedia: https://upload.wikimedia.org/wikipedia/commons/c/cb/BackyardParty.jpg |
So setzt sich die Reihe mit Gast Nummer vier, fünf, und so weiter fort, und in jeder Runde reduziert sich die Anzahl der verbleibenden Tage, und damit der Zähler der Division um den Wert Eins, deren Ergebnis zur Wahrscheinlichkeit der letzten Runde hinzumultipliziert wird.
01 #!/usr/bin/env python3
02
03 dates = 365
04 dates_left = dates
05 prob = 1
06
07 for person in range(1,24):
08 prob=prob*dates_left/dates
09 print("%2d: %.4f" % (person, 1-prob))
10 dates_left -= 1
Listing 1 zeigt eine schlanke Python-Implementierung der Berechnung. In der Ausgabe in Abbildung 2 zeigt sich in der Tat, dass beim 23. Gast die 50%-Marke der Wahrscheinlichkeit einer Geburtstagsdoublette mit 50,73% überschritten wurde. Dabei setzt das Skript die Anzahl der im Kalender verbleibenden Tage anfangs auf 365 und zieht nach jeder Runde den Wert Eins davon ab, da wieder ein Gast mit einem noch nicht gesehenen Geburtstag erschienen ist. Die Wahrscheinlichkeit prob gibt an, wie die Chancen stehen, dass keiner im Raum mit einem andern den Geburtstag teilt, bei einem Raum mit nur einer Person ist dies 1, bei zweien 0,9973. In jeder Schleifenrunde multipliziert Listing 1 den Wahrscheinlichkeit der letzten Runde in prob mit dem hinzugekommenen Wahrscheinlichkeitswert und weist das Ergebnis wieder prob zu. Gewünscht wird jedoch nicht die Wahrscheinlichkeit keiner Geburtstagskollision, sondern das Gegenteil, die Chance auf ein Zusammentreffen, deshalb gibt Zeile 9 zur aktuellen Gastzahl jeweils die Wahrscheinlichkeit des gegenteiligen Ergeignisses an, also 1-prob für die Chance auf eines oder mehrere Geburtstagspaare auf der Party.
 |
| Abbildung 2: Das Skript errechnet die Wahrscheinlichkeit eines Geburtstagspaares für verschiedenen Gästezahlen aus. |
Ob die Formel für die Berechnung richtig war oder nicht, soll nun ein Simulationsskript zeigen, das pro Runde 23 Gäste in der Liste guest_bdays einer Party zuordnet, jedem von ihnen aus 365 Integerwerten einen zufälligen Geburtstag zuweist und anschließend in der Funktion bday_match aussortiert, ob in guest_bdays irgendwelche Integer-Duplikate vorliegen. Die Funktion randint aus dem Modul random spuckt für die Geburtstage der Gäste Werte zwischen den beiden Extremen 1 und 365 (einschließlich) aus.
01 #!/usr/bin/env python3
02
03 import random
04
05 def bday_match(bdays):
06 seen = set()
07 for bday in bdays:
08 if bday in seen:
09 return True
10 seen.add(bday)
11 return False
12
13 for epoch in range(10):
14 parties = 100000
15 matches = 0
16 nof_days = 365
17 nof_guests = 23
18
19 for party in range(parties+1):
20 guest_bdays=[]
21 for _ in range(nof_guests):
22 bday = random.randint(1,nof_days)
23 guest_bdays.append(bday)
24
25 if bday_match(guest_bdays):
26 matches += 1
27
28 print(matches/parties)
 |
| Abbildung 3: Das Simulationsskript mit 23 Personen schießt sich auf etwa 53% Überlappungswahrscheinlichkeit ein. |
Die For-Schleife ab Zeile 13 iteriert dazu über insgesamt 10 Testläufe mit jeweils 100.000 Parties, und zu jeder Veranstaltung, bei der ein Geburtstagspaar auftritt, erhöht sich der Zähler matches um 1. Am Ende jedes Durchlaufs druckt das Skript den Quotienten aus der Anzahl der Parties mit Geburtstagspaaren zur Gesamtzahl der Parties aus, und Abbildung 3 zeigt, dass sich der Wert bei etwa 50.7% einpendelt.
Die Funktion bday_match ab Zeile 5 nimmt eine Python-Liste mit Integern entgegen und prüft, ob sich darin ein oder mehrere Duplikate befinden. Effizient geht dieser Test, indem die Funktion bereits gesehene Werte in einem Set seen mit einer Hash-Funktion häckselt, weil sie dann bei jedem neu untersuchten Wert blitzschnell nachsehen kann, ob der Wert schon im Set ist. Wer diese Aufgabe schon einmal bei einem Einstellungstest bekam, weiß, dass die Rechenzeit der Duplikatsprüfung mit diesem Verfahren bei N Listenelementen auf O(N) absinkt, während sie bei einer weniger cleveren Zwei-Schleifen-Lösung O(N**2) betrüge.
Wie entwickelt sich der Wert für die Wahrscheinlichkeit einer Geburtstagskollision mit steigender Gastzahl? Dank der Python-Bibliothek matplotlib, einfach installiert mittels pip3 install --user matplotlib, produziert Listing 3 mit den Ausgabedaten von Listing 1 den Graphen in Abbildung 4:
./birthday-paradox | ./bd-plotMittels des speziellen File-Handles sys.stdin liest Listing 3 dabei die Ausgabezeilen von Listing 1 und spaltet sie mit der split-Methode in Zeile 10 am Doppelpunkt, der Gastzahl und Wahrscheinlichkeit trennt. Für die X- und Y-Werte im Graphen baut es die Listen x und y zusammen, in dem es für jedes Wertepaar den neuesten Wert mittels der append-Methode an die jeweilige Liste anhängt. Die plot-Methode nimmt dann alle X- und Y-Werte gesammelt entgegen und zeichnet den Graphen, den die Methode savefig in Zeile 18 in eine PNG-Bilddatei schreibt. Mit weniger Aufwand geht es kaum, und der Graph sieht ausgesprochen ansprechend aus.
01 #!/usr/bin/env python3
02
03 import matplotlib.pyplot as plt
04 import sys
05
06 x=[]
07 y=[]
08 for line in sys.stdin:
09 (guests,prob)=line.split(': ')
10 x.append(guests)
11 y.append(prob)
12
13 plt.plot(x,y)
14 plt.xlabel('Guests')
15 plt.ylabel('Probability')
16
17 plt.savefig('bd-collision.png')
 |
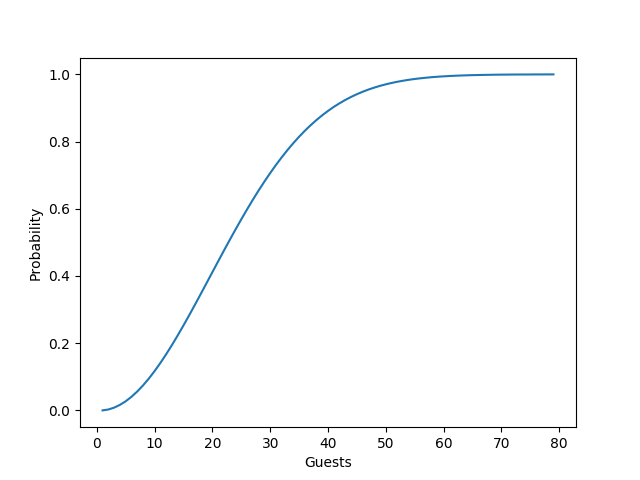| Abbildung 4: Wahrscheinlichkeit gleicher Geburtstage bei steigender Gastzahl. |
Was übrigens bei einer Party mit 100 Teilnehmern passiert, lässt sich ebenfalls mit den Skripts in dieser Ausgabe ermitteln: Zu 99,99996928% tanzt dort ein Geburtstagspaar, die Chance, dass bei dieser Mega-Party alle Gäste unterschiedliche Geburtstage haben beträgt mehr als Eins zu drei Millionen.
Listings zu diesem Artikel: http://www.linux-magazin.de/static/listings/magazin/2018/03/snapshot/
Youtube-Video "The Birthday Problem/Paradox": https://www.youtube.com/watch?v=QrwV6fJKBi8
 |
Michael Schilliarbeitet als Software-Engineer in der San Francisco Bay Area in Kalifornien. In seiner seit 1997 laufenden Kolumne forscht er jeden Monat nach praktischen Anwendungen verschiedener Programmiersprachen. Unter mschilli@perlmeister.com beantwortet er gerne Ihre Fragen. |
Hey! The above document had some coding errors, which are explained below:
Unknown directive: =desc